Unit Circle- Understanding Its Significance in Math
If you’re studying or preparing for trigonometry, you’ll need to know the unit circle. This circle serves as an essential tool used to solve angular sines, cosine, and tangents, ultimately the lengths of triangles. How do they work, and what information is required to use it? This article describes the unit circle and its usage in more detail.
What is a Unit Circle?

A unit circle is typically drawn around the origin (0,0) of a X,Y axes with a radius of 1. For a straight line drawn from the circle’s centre point to a point along the circle’s edge, the length of that line is always 1. This also means that the circle’s diameter is equal to 2 because the diameter is equal to twice the length of the radius. Usually, the unit circle’s centre point is the point where the x-axis and y-axis intersect, or at the coordinates (0,0).
This is a triangulation concept that allows mathematicians to extend sine, cosine, and tangent by frequency outside the traditional right triangle. As you remember, sine, cosine, and tangent are the ratio of the sides of a triangle to a given angle, commonly referred to as theta.
Sine = the ratio of the length of the opposite side of the right triangle to the hypotenuse.
Cosine = the ratio of the length of the adjacent leg of the right triangle to the hypotenuse’s length.
Tangent = the ratio of the length of the opposite leg to the length of the adjacent leg.
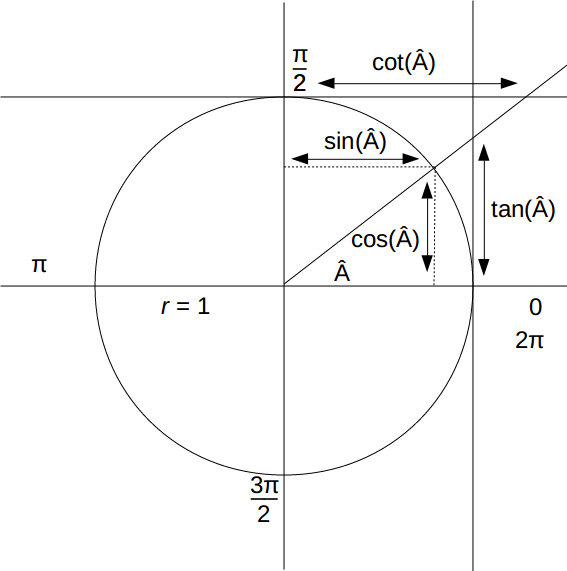
Use these traditional definitions to limit the description of angles in the right triangle from 0 to 90 degrees. In some cases, you need to know these values for angles greater than 90, and the unit circle makes that possible.
These are named so because they have a radius of one unit. Its center is at the origin, and all points around the circle are one unit away from the centre. If you draw a line from the centre to a point on the circumference, the line’s length will be 1. You can then add a line to create a right triangle. This triangle will have a height equal to the y coordinate and whose length is similar to the x coordinate.
Understanding Its Use
As mentioned above, the unit circle allows you to quickly solve any order or radian sine, cosine, or tangent. Knowing the graph of the circle is especially useful if you need to solve a particular trigger value.

Here are some tips to memorize. These tips make it easy to use for math problems that require a unit circle.
Memorize common angles and coordinates: To use the unit circle effectively, you need to remember the most common angles (both degrees and radians) and their corresponding x and y coordinates.
Find out what is negative and positive.
To find the correct value for the trigger problem, it is important to distinguish between positive and negative x and y coordinates.
How to Solve Tangent
Finally, it is essential to know how to use all this information about triangulation circles, sines and cosines to solve the tangents of angles.
Above all, review our math resources and others for additional help on this useful trigonometric tool.