Interval Notation – How and Where to Use It
In mathematics, we want to be as efficient and accurate as possible when explaining certain principles. One such example is the interval notation. An interval is a range of real numbers between a and b in a <b that contains all real numbers from the specified start point a to the specified endpoint b. This notation frequently shows up in Algebra and other advanced math when displaying an interval.

Interval notation describes the set containing all real numbers between the lower and upper bounds, which might not be included. Endpoint values are listed in parentheses/brackets. Square brackets indicate they lie within the set, and parentheses indicate they don’t lie within the set. For example given (3,15], 3 is not included while 15 is.
Interval Notation Types
There are several different types of intervals, called open intervals and closed intervals, which commonly occur when studying mathematics, called (a, b) and [a, b], respectively.
- Open
Open interval uses parentheses. This means that the range contains all real numbers x that is precisely between the numbers a and b. That is, the range does not actually have the numbers a and b. Another way to indicate the open interval is for all sets of x such that a <x <b.
- Close
For closed ranges, square brackets indicate that the endpoints lie within the range. Therefore, closed intervals can be annotated as a set of a ≤ x ≤ b.
Half Open Interval
A slightly more complex interval is called the half-open interval, shown as (a, b] and [a, b). These are their respective sets of all x, such as a < x < b, and a ≤ x ≤ b. For every point x in the interval, if there is an actual positive number M with the following properties, the interval is limited like x | <M.
Calculation and Interval
Intervals occur regularly in calculus. The interval at which the function is defined, such as the intermediate value theorem, is closed and delimited. Closed and separated intervals touch on compactness, which is one of the most critical concepts in the broader study of computation. Many of the core theories of computation revolve around compact sets. A compact set is a precisely closed boundary spacing in a real setting.
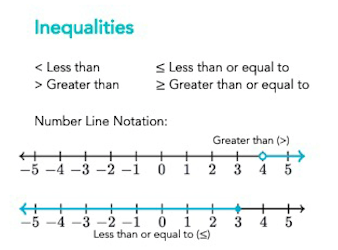
The spacing notation is a simplified form that describes a solution to inequality or system of inequalities, using parentheses and brackets instead of the inequality symbol. The range in parentheses is called the open range. This means that the variable cannot have an endpoint value.
For example, solution 3 <x <5 is written as (3,5) in interval notation because x cannot be equal to 3 or 5. Determines the lower and upper limits of the variable.
How to describe the set of values
- Identify where the thick line overlaps the actual line to determine what to include in the set.
- At the left end of each range, use [. Each end value is included in the set (solid dot) or (for each excluding end value (white dot)).
- At the right end of each range, use] to include each end value in the set (full dot) or) each excluded end value (white dot).
Determine the value of the variable that makes the inequality true. For example, the value of x that makes the inequality 3x-6 <3 true is x <2.
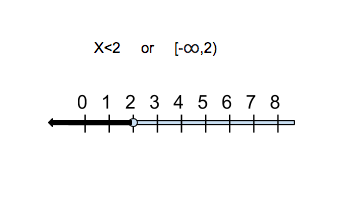
Graph these values on a line using open points for < and >, and closed points for ≤ and ≥. In the above example, an open point is drawn at 2 on the number line, and an arrow pointing to the left of the number line is drawn to indicate x <2.
The lower bound of a variable is marked with the left square bracket “[” if the variable can have that value, or with the left bracket “(” if it cannot or the lower bound is negative infinity. Then, since x is negative infinity, the lower limit is described as “(-∞”.
Write a comma after the lower bound, then the upper bound of the variable, and if the variable can contain its value, but the right bracket “]”, if not, or if the upper bound is positive, the right bracket “)” is described. In the above example, the upper limit is 4, and x cannot have that value, so write “, 4)” and give the answer in interval notation (-∞, 4) meaning a range of numbers from negative infinity to 4.’
Union Symbol
Lastly, if the variables have other spacing, connect them with the union symbol “v”. Arrange the intervals from minimum to maximum. For example, if x ≥ 6 is another solution to the inequality in this example, write (-∞, 3) v [6, ∞) as the interval notation.
For additional help, check out some of our Gooroo courses on math!
Written By: Anonymous Gooroo Blogger